Exemples
Le pgcd de deux nombres entiers positifs n1 et n2 est leur plus grand diviseur commun. On suppose : n1 ≥ n2 :
Exemple : PGCD de 30 et 8 = 2
L'algorithme est basé sur la division euclidienne :
a=b * q + r avec r < b
PGCD(a,b) = PGCD(b,r)

-
Lire les deux entiers naturels a et b
-
r ← a div b
-
Si R est différent de 0 alors
a ← b
b ← r
revenir au point 2
sinon
pgcd ← b
-
Afficher le résultat : pgcd
On désire calculer un salaire net d'un employé à partir du salaire horaire brut, du nombre d'heures effectuées et du pourcentage de charges à retenir sur le salaire brut.
Données :
-
SH : le salaire horaire
-
NH : le nombre d'heures
-
PR : le % de retenues
Calculer : SB ← SH * NH { le salaire de base }
R ← SB * PR : { les retenues }
SN ← SB - R : { le salaire net }
Ecrire le résultat :
"Salaire net" = SN
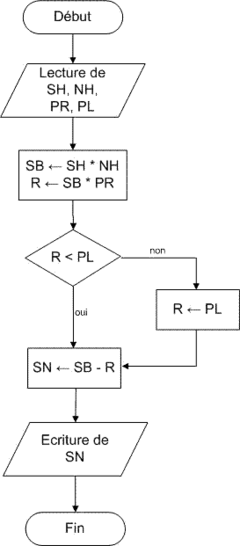
Cette fois-ci, on introduit un plafond pour les charges retenues sur le brut. On écrit alors un algorithme avec condition. En cas de dépassement du plafond, on ne retient que le plafond.
Données :
-
SH : le salaire horaire
-
NH : le nombre d'heures
-
PR : le % de retenues non plafonnées
-
PL : le plafond
Calculer :
SB ← SH*NH { le salaire de base }
R ← SB*PR { les retenues }
Si R > PL alors R ← PL
SN ← SB-R { le salaire net }
Ecrire le résultat :
"Salaire net" = SN
On peut également représenter cet algorithme sous la forme d'un organigramme, comme indiqué ci-après :